
周期矩形脉冲信号的频谱
例2 设周期矩形脉冲信号f(t)的脉冲宽度为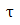 ,脉冲高度为E,重复周期为T,如图3-13所示。设该信号在一个周期(-T/2
,脉冲高度为E,重复周期为T,如图3-13所示。设该信号在一个周期(-T/2

根据
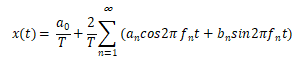
计算结果:
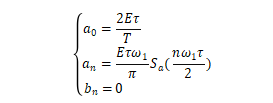
这样周期矩形信号的三角形傅里叶级数为
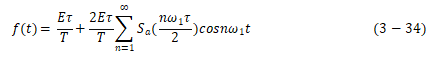
若给定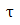 ,T,E,就可以求出直流分量,基波和各次谐波分量的幅度:
,T,E,就可以求出直流分量,基波和各次谐波分量的幅度:
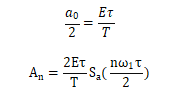
将各分量的幅度和相位用垂直线段在频率轴的相应位置上标示出来,就是信号的频谱图,如图3-14所示。
综上所述,可以看到周期矩形脉冲频谱具有如下特点:
1)周期矩形脉冲的频谱是离散的线状频谱,谱线只出现在ω1的整数倍频率,即各次谐波频率上。两条谱线的间隔为ω1(等于2π/T)。谱线间隔与T成正比,当脉冲重复频率增大时,谱线将靠近。
2)各谱线的幅度包络线按照抽样函数Sa (nω1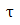 /2)的规律变化。当(nω1
/2)的规律变化。当(nω1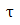 /2)为π的整数倍,即
/2)为π的整数倍,即 时,谱线的包络线经过零点。当ω
=0,3π/
时,谱线的包络线经过零点。当ω
=0,3π/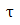 ,5π/
,5π/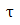 时,谱线的包络线为极值点。
时,谱线的包络线为极值点。
3)周期矩形脉冲信号包含无穷多条谱线。随着频率的增高,谱线幅度变化的总趋势呈收敛状,但其主要能量集中在第一零点以内。实际上,在允许一定失真的条件下,可以舍弃ω>(2π/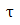 )的频率分量,而把ω=0~(2π/
)的频率分量,而把ω=0~(2π/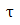 )这段频率范围称为矩形脉冲信号的占有频带宽度。记作B或Bf,
B=2π/
)这段频率范围称为矩形脉冲信号的占有频带宽度。记作B或Bf,
B=2π/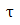 ,或Bf=1/
,或Bf=1/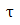 。
。
由此可见,频带宽度B只与脉宽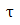 有关,而且两者之间为反比关系。这种信号的频宽与时宽成反比的性质是信号分析中最基本的特性。
有关,而且两者之间为反比关系。这种信号的频宽与时宽成反比的性质是信号分析中最基本的特性。
4)直流、基波及各次谐波分量的幅度正比于脉宽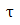 ,反比于周期T;并且当周期增大时,谱线变密。
,反比于周期T;并且当周期增大时,谱线变密。
5)如果将正负频率的谱线都画出,则每个分量的幅度一分为二,只有把正、负频率上对应的两条谱线加起来才代表一个分量的幅度。应当指出,负频率的出现完全是数学运算的结果,并无任何物理意义。
以上特点是由分析周期矩形脉冲频谱得到的,基本上也适用于其他周期信号。
灵科超声波坚持自主研发,最大力度投入研发设计,拥有一支近30年的研发制造团队,发明创造170余项专利新技术。主要品牌有LINGGAO灵高、LINGKE灵科、SHENGFENG声峰等。广泛运用在医疗器械、电子器材、 打印耗材、塑料、无纺布、包装、汽配等多个领域,为海内外各行业、企业提供了大量稳定性强的优质超声波塑焊设备及应用方案。