某些物理现象需要用一个时间极短，但取值极大的函数模型来描述。例如，力学中的瞬间冲击力，电学中的雷击电闪，数字通信中的抽样脉冲等。“冲激函数”的概念就是以这类实际问题为背景而引出的。

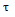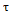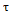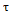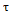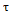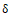冲激函数可由不同的方式来定义。首先分析矩形脉冲如何演变为冲激函数。图4-2a给出了宽为 ，高为1/ 的矩形脉冲，当保持矩形脉冲面积 (1/ )=1不变，而使脉宽趋近于零时，脉冲幅度必趋于无穷大，此极限情况即为单位冲激信号，常记作 , 又称为“ 函数”。

单位冲激函数用箭头表示，如图4-2b所示。它表明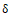：(t) 只在t=0点有一“冲激”，在t=0点以外各处函数值都是零，且冲激的面积为1。即对于任意实数，t≠0时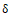(t)＝0， 且 。

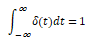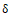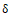如果矩形脉冲的面积不是固定的1，而是a，则表示一个冲激强度为a倍单位值的 函数，即a (t),

如果单位冲激信号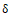 (t)与一个在t=0点连续的信号f(t)相乘，则乘积仅在t=0处得到f(0) 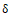(t)其余各点的乘积均为零，于是对于冲激函数有如下性质：

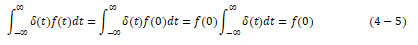
类似地，对于延迟t₀的单位冲激信号有

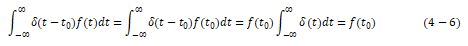
以上两式表明了冲激信号的抽样特性(或称“筛选”特性）。根据这一特性，可以将任意的连续时间信号表示为无穷多个不同时间延迟t 的冲激信号的加权积分，即将任意信号分解为无穷多个冲激信号的叠加，这体现了信号分解的思想。

将连续信号f(t)近似分解为如图4-3所示的矩形脉冲之和。当t=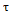时，连续信号近似为图中阴影部分所示的矩形脉冲信号。当脉冲宽度 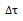趋近于零时，这个脉冲信号可近似看做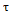时刻的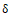 函数，这个冲激函数的强度（面积）为f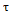（ ）。因此可将f（t）分解为无穷多个强度不同的 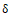函数的叠加，即

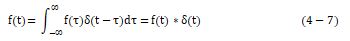
对于任一LTI系统，当该系统的输入为一单位冲激信号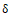 (t),时，此时系统的输出可以唯一确定地表征该系统，这个输出被称为系统的单位冲激响应h(t)。如果将系统的输入x(t)分解为无穷多个强度不同的 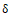函数的叠加，根据LTI系统的非时变性和线性，输出信号可表示为无穷多个强度不同的冲激响应h(t)的叠加，则系统的输出y(t)就可表示为

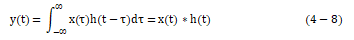
所以，如果知道了LTI系统的单位冲激响应h(t),那么对于任一输入x(t),都可以通过上式求得输出y(t),即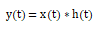。从而单位冲激响应h(t)可完全表征线性非时变系统的特性。

在反射法超声检测过程中，带有缺陷信息的试件或反射体就可看做系统，超声波的入射可视为系统的输入，反射波可视为系统的输出。当然，具有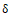 函数性质的入射超声波是不可能得到的，因为没有如此理想的超声波换能器可以发射持续时间趋近于零的超声波脉冲。即使可以实现，那么入射的超声波也会因能量太小而迅速衰减掉。所以，通常无法直接得到唯一确定表征被测试件特性的单位冲激响应h(t)。但通过一种基于频谱分析的数据处理方法，可以间接得到试件的单位冲激响应，极大提高了检测分辨力。

灵科超声波坚持自主研发，最大力度投入研发设计，拥有一支近30年的研发制造团队，发明创造170余项专利新技术。主要品牌有LINGGAO灵高、LINGKE灵科、SHENGFENG声峰等。广泛运用在医疗器械、电子器材、 打印耗材、塑料、无纺布、包装、汽配等多个领域，为海内外各行业、企业提供了大量稳定性强的优质超声波塑焊设备及应用方案。