加零处理

为了便于对序列x(nT_s)进行FFT处理，希望采样序列长度N是2的整数次幂。而按前面方法确定的N一般不满足这个条件，为此，通常用给x(nT_s)加零的办法，使

式中，P是正整数; N_x是加零点数。

此外，信号经过FFT后得到的频谐是离散的谱线，谱线间隔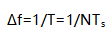。因此，用离散傅里叶变换来观看频谐，只能通过一个“栅栏”来观看，即只能在离散点处看到真实的频谱。如果一个频率分量恰巧落在两个离散谱线之间，这个频率分量就会看不到，这称为“栅栏效应”。为了克服该效应对频率分辨力的影响，可在原信号的末端补加一些零，这相当于人为地增加了时域截断长度T,也就能在频谱形式不变的情况下，变更谱线的位置，减小谱线间隔，以便有可能看到原来看不到的频谱分量(见图3-6）。所以，加零可以提高频率分辨力。

频谱分析常用定理

频谱分析中经常要用到一些频谱定理，其实质是傅里叶变换的某些性质，它反映了信号同其频谱之间的基本关系，常用的频谱定理包括:

(1)线性叠加定理   如果x(t)和y(t)分别有傅里叶变换X(f)和Y(f),则它们的和x(t)+y(t)有傅里叶变换X(f) + Y(f),如图3-7所示。

(2)对称或对偶定理   若时域函数x(t)对应频谱为F(f),即x(t)⟷ F(f)，则有

(3)时间展缩定理    如果x(t)的傅里叶变换是F(f)，则x(kt)的傅里叶变换对为

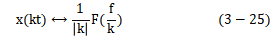
在科学技术的许多领域，傅里叶变换的时间尺度变化这一性质为大家所熬悉，如图3-8所示，时间尺度扩展(或压缩)h倍，相应于频率尺度压缩(或打辰)h倍。应当指出，当时间尺度扩展时，不仅频率尺度缩小，而且频率域里的垂直幅度增大，使曲线下的面积保持不变。在用磁带机作扩展时间轴和压缩时间轴的频谱分析中，这是一个具有实用价值的方法。

a)时间没有扩展    b）时间放慢2倍，k=1/2   c）时间放慢4倍，k=1/4

(4)频率展缩定理   如果F(f)的傅里叶变换是x(t)，k是实数，则F(kf)的傅里叶变换可由下面傅里叶变换对给出:

与时间尺度改变相类似，频率尺度扩展(或压缩)k倍，将导致时间尺度压缩(或扩展)k倍。这个效应如图3-9所示。当频率尺度扩展时，时间函数的幅度就增大。

(5)时间位移——时移定理   如果x(t)的自变量t被移动一个常量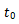 ,则可

图3-9 频率尺度变化性质

a）频率没扩展  b）频率展缩为1/2，k=1/2   c)频率展缩为1/4，k=1/4

得到

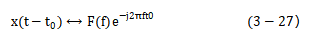
这个变换对的图解如图3-10所示。可以看出，由于时间位移而引起了相角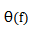 的变化，即

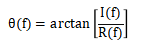
图3-10时间位移性质

a)没有时移时

图3-10 时间位移性质(续)

b)时移45°时   c）时移90º时   d）时移180°时

应该指出，时间位移并不改变傅里叶变换频域幅值的大小。