上一篇文章中 ，我们了解到了超声波的定义，下面我们将会从超声波的基本物理量、连续波和脉冲波解析，进一步帮助读者理解超声波频谱分析技术。

描述超声波的基本物理量

声速：单位时间内，超声波在介质中传播的距离，用符号“C”表示。

频率：单位时间内，超声波在介质中任一给定点所通过完整波的个数，用符号“f ”表示。

波长：声波在传播时，同一个波线上相邻两个相位相同的质点之间的距离，用符号“λ”表示。

周期：声波向前传播一个波长距离时所需的时间，用符号“T”表示。

角频率：以符号“ω”表示，定义为ω=2π/T=2πf。

上述各参量之间的关系为

连续波和脉冲波

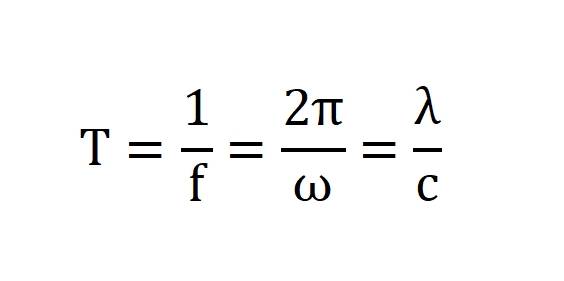
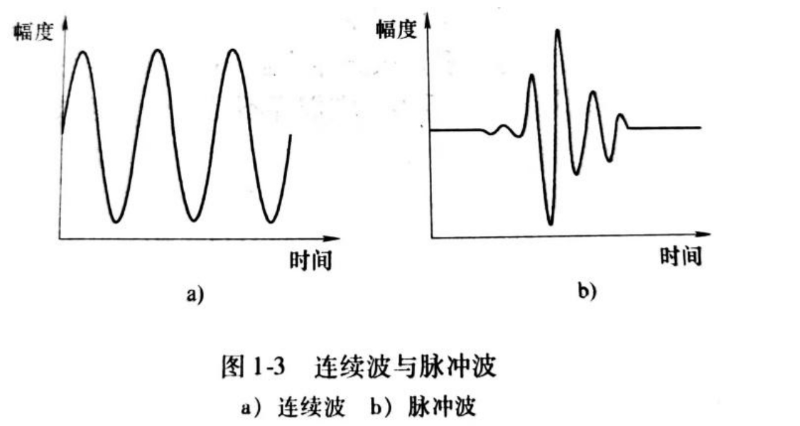
根据持续时间的长短，超声波可以分为连续波和脉冲波。连续波指介质中质点振动持续时间为无穷的波动，如图1-3a所示。脉冲波是指振动持续时间有限（单个或间发）的波动，如图 1-3b所示。

按照傅里叶分析方法可知，一个脉冲波可以分解为多个不同频率谐振波的叠加，如图1-4所示。可以看出，以时间为自变量的一个复杂波形，其实包含着一系列不同频率的正弦（或余弦）波，这些频率成分及其幅度均可以在频域中给出清晰的描述。    

图1-5给出了超声检测中1MHz 的脉冲波与其中包含的正弦波之间的关系。可以看出，此处1MHz 的脉冲波由 0.85MHz、1MHz和 1.21MHz 正弦波叠加而成[4 ] 。为合成某一脉冲，需要一系列的正弦波，且要合成的脉冲宽度越窄，需要的正弦子波数量越多。这些子波具有与中心频率不同的频率。由于子波的频率不同，因此在传播条件不合适时会产生畸变，通常使脉冲宽度变宽。

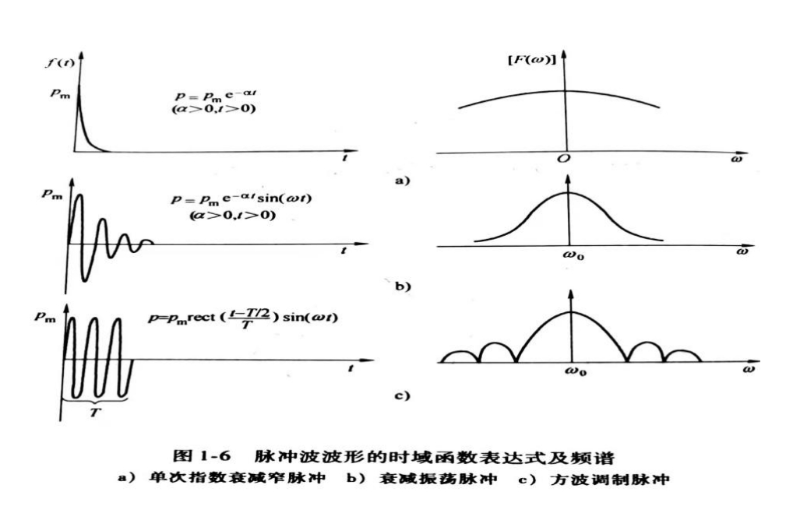
超声学中常用的脉冲波波形主要有单次指数衰减窄脉冲，衰减振荡脉冲和方波调制脉冲。图1-6 给出了上述三种形式脉冲波波形的时域函数表达式及由傅里叶变换得到的频谱示意图。可以看出，它们都不是一个单频波，在其基频附近存在一个频带。

关注灵科超声波 ，我们将会在下个章节中对节对超声脉冲波的频率和超声脉冲波的声场进行讲解与分析。