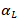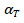和 的相应变量可通过独立散射模型的微分来计算:

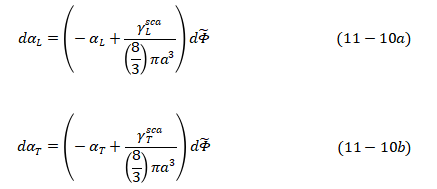
式中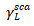，和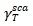 分别是纵波和横波传播过程中的散射横截面，导致声波散射的粒子均匀地分布于被测样品中。

当研究纵波衰减时，可以应用在前文讨论的基础上简化后的微分方程，其基本方程归纳如下：

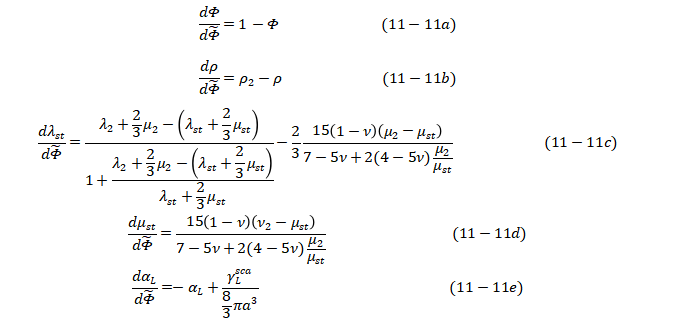
结合式(11-10)，其中

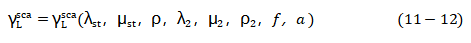
那些方程可以通过参数和初始条件

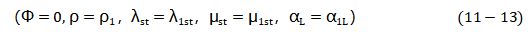
来求解。

实验中所用的材料为玻璃颗粒增强的环氧复合材料和玻璃颗粒增强的聚酯复合材料。这两种材料的粘滞性、相速度和衰减系数见表11-2，其中相速度是和频率无关的常数，而衰减系数是频率的一次函数。

对于环氧复合材料中的球形玻璃颗粒而言，它的计算归一化散射横截面积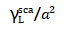是归一化参数 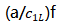的函数，这个参数表示着颗粒半径a和基体中的波长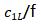的比率。图11-6中实曲线是考虑基体粘滞性时的归一化散射体的横截面，而虚线是没有考虑基体粘滞性时的归一化散射体的横截面。

从图11-13中可以看出，这两条曲线忽略了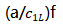标绘范围的差异。聚酯基体中的玻璃颗粒物有相同特征，因为环氧(树脂）和聚酯有相同的声学性质。因此，在计算上面提到的散射体的横截面积时，用（模量的）实部值代替复合模量值是合理的。

灵科超声波坚持自主研发，最大力度投入研发设计，拥有一支近30年的研发制造团队，发明创造170余项专利新技术。主要品牌有LINGGAO灵高、LINGKE灵科、SHENGFENG声峰等。广泛运用在医疗器械、电子器材、打印耗材、塑料、无纺布、包装、汽配等多个领域，为海内外各行业、企业提供了大量稳定性强的优质 超声波塑焊设备及应用方案 。