此处给出的公式与Beltzer和Brauner、Biwa等人针对纤维复合材料提出的公式类似。尽管按照颗粒(浓度)的允许范围，很难来评价微分法的有效性，但是该模型已有很大改进，它可以解释稀浓度模型无法解释的复合材料的宏观性质。

当颗粒物体积分数的增量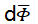 为无穷小量且刚刚分散到复合材料中时，根据混合定律，复合材料的密度变化为

此外，根据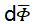 的相对增量，绝对的颗粒物体积分数Φ增加量为

各向同性粘滞性材料的复合模量，可以通过固体中纵波和横波的相速度和衰减系数的形式来给出。若纵波和横波的相速度和衰减系数分别为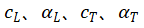 ，则λ 和μ可由下式给出：

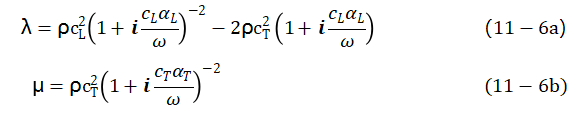
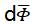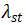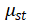式中，ω为角频率。如文献所述，由于增量 引起的等效介质的 和 的改变可以根据 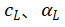和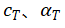 的变化来给出公式。此外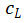， 和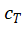 是和频率无关的，可以基于 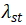和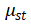 的实数值给出如下形式：

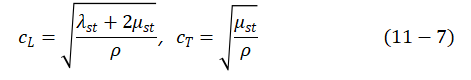
目前，在声衰减模型中，相速度的影响占次要地位，故而本文忽略了相速度与频率之间的相关性。热而需要注意的是，利用Kramers-Kronig关系，这种效应可以非常容易地被体现出来。

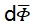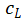由于 造成的 和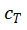 的变化可以利用 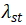和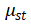 的变化量来计算，用公式表示为

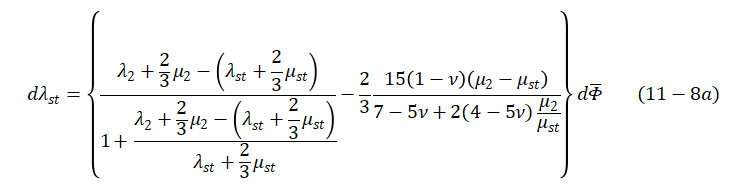
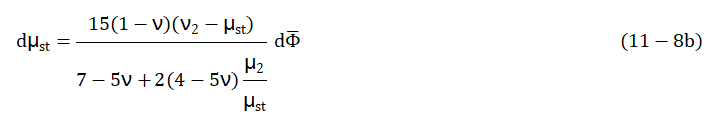
其中

是复合材料的泊松比。

灵科超声波坚持自主研发，最大力度投入研发设计，拥有一支近30年的研发制造团队，发明创造170余项专利新技术。主要品牌有LINGGAO灵高、LINGKE灵科、SHENGFENG声峰等。广泛运用在医疗器械、电子器材、打印耗材、塑料、无纺布、包装、汽配等多个领域，为海内外各行业、企业提供了大量稳定性强的优质超声波塑焊设备及 应用方案。